9.4.9 Delimiters

Placing brackets around a tall object in maths mode, such as fractions, does not look right if you use normal sized brackets. For example:

\[
(\frac{1}{1+x})
\]

results in:

$Image: normal sized brackets around fraction.$

Instead, you can automatically resize the delimiters using the commands:

\left<delimiter>

and

\right<delimiter>

Rewriting the above example:

\[ \left( \frac{1}{1+x} \right) \]

produces:

$Image: brackets now the same size as the fraction.$

Note that you must always have matching \left and \right commands, although the delimiters used may be different. If you want one of the delimiters to be invisible, use a . (full stop) as the delimiter. Available delimiters are shown in Table 9.13. (Note for a vertical bar delimiter it's best to use amsmath's \lvert command instead of | and \lVert instead of \|.) Sometimes using \left and \right doesn't produce the optimal sized delimiters. In which case you can use additional commands provided by the amsmath package shown in Table 9.14.

**Table 9.13:** Delimiters (^†defined by `amsmath`)
`(`	`)`	`[`	`]`
`\{`	`\}`	`\lvert^†`	`\rvert^†`
`\lVert^†`	`\rVert^†`	`\langle`	`\rangle`
`\lfloor`	`\rfloor`	`\lceil`	`\rceil`
`\uparrow`	`\downarrow`	`\Uparrow`	`\Downarrow`
`\updownarrow`	`\Updownarrow`	`/`	`\backslash`

**Table 9.14:** Additional Commands Provided by `amsmath` for Delimiter Sizing
Definitions		Example
Default Size		$( X )$
`\bigl<delim>`	`\bigr<delim>`	$\bigl( X \bigr)$
`\Bigl<delim>`	`\Bigr<delim>`	$\Bigl( X \Bigr)$
`\biggl<delim>`	`\biggr<delim>`	$\bigl( X \biggr)$
`\Biggl<delim>`	`\Biggr<delim>`	$\Biggl( X \Biggr)$

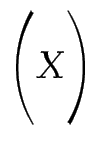
Example (Vertical Bar Delimiters):

\[
\left\lvert
\frac{1}{1+x}
\right\rvert
\]

$Image: vertical bars same height as fraction.$

Example (Delimiter with Subscript):

Delimiters can take limits:

\[
\left\lvert
\frac{1}{1+x}
\right\rvert_{x=0}
\]

Image: as before but the right vertical bar has a subscript.

Example (Mismatch):

The left and right delimiters don't have to match:

\[ \left[\frac{1}{1+x}\right\rangle \]

$Image: large open square bracket followed by fraction followed by large right angle bracket.$

Example (An invisible delimiter):

Every \right must have a matching \left (and vice versa), so use a . (full stop) for an invisible delimiter.

\[ \left. \frac{\partial f}{\partial x} \right\rvert_{x=0} \]

$Image: partial fraction followed by large vertical line with a subscript.$

We have now covered enough to reproduce the equation shown in §1. Introduction:

Image showing a second order partial derivative.

Note:

The above code looks a bit complicated, and there are so many braces that it can be easy to lose track, so here are some ways of making it a little easier to type:

Whenever you start a new environment type in the \begin and \end bits first, and then insert whatever goes inside the environment. This ensures that you always have a matching \begin and \end. The same goes for \[ and \].
Whenever you type any braces, always type the opening and closing braces first, and then insert whatever goes in between. This will ensure that your braces always match up.

So keeping these notes in mind, let's try typing in the code in a methodical manner:

Start and end the displayed maths mode:

\[
\]
We now need a partial derivative. (The command \pderiv is defined as described earlier. Make sure you remember to define it, preferably in the preamble .)

\[
\pderiv{}{}
\]
Let's do the first argument. This partial derivative is actually a double derivative, which means we need a squared bit on the top along with a calligraphic L:

\[ \pderiv{^2 \mathcal{L}}{} \]
The second argument is the $z_i^\rho$ squared bit. This is a nested superscript {z_i^\rho}^2:

\[ \pderiv{^2 \mathcal{L}}{{z_i^\rho}^2} \]
We can do the next partial derivative in the same way. This one is slightly easier to do:

\[
\pderiv{^2 \mathcalL}{{z_i^\rho}^2} =
-\pderiv{\rho_i}{z_i^\rho}
\]
Delimiters also need to occur in pairs, like curly braces and \begin and \end, so let's do them next:

\[
\pderiv{^2 \mathcal{L}}{{z_i^\rho}^2} =
-\pderiv{\rho_i}{z_i^\rho}
\left(
\right)
\]
Now we need to do the bits inside the brackets. First of all we have yet another partial derivative:

\[
\pderiv{^2 \mathcal{L}}{{z_i^\rho}^2} =
-\pderiv{\rho_i}{z_i^\rho}
  \left(
    \pderiv{v_i}{\rho_i}
  \right)
\]
Now we have a fraction following the partial derivative from the previous step. (Make sure you use braces for the exponential bit: \e^{v_i} ( $\mathrm{e}^{v_i}$ ) is not the same as \e^v_i ( $\mathrm{e}^v_i$ ). The command \e is defined as described earlier. Make sure you define it, preferably in the preamble .)

\[
\pderiv{^2 \mathcal{L}}{{z_i^\rho}^2} =
-\pderiv{\rho_i}{z_i^\rho}
  \left(
    \pderiv{v_i}{\rho_i} \frac{\e^{v_i}}{1-\e^{v_i}}
  \right)
\]
This is followed by 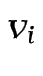times another fraction:

\[
\pderiv{^2 \mathcal{L}}{{z_i^\rho}^2} =
-\pderiv{\rho_i}{z_i^\rho}
  \left(
    \pderiv{v_i}{\rho_i} \frac{\e^{v_i}}{1-\e^{v_i}}
    + v_i \frac{}{}
  \right)
\]
The bottom part of the fraction (the denominator) is easier than the top, so let's do that first:

\[
\pderiv{^2 \mathcal{L}}{{z_i^\rho}^2} =
-\pderiv{\rho_i}{z_i^\rho}
  \left(
    \pderiv{v_i}{\rho_i} \frac{\e^{v_i}}{1-\e^{v_i}}
    + v_i \frac{}{(1-\e^{v_i})^2}
  \right)
\]

Now for the top part of the fraction (the numerator). To refresh your memory, it should look like:

$\displaystyle \mathrm{e}^{v_i}\frac{\partial v_i}{\partial \rho_i}(1-\mathrm{e}^{v_i}) + \mathrm{e}^{2v_i}\frac{\partial v_i}{\partial \rho_i}$

That's a bit complicated, so let's break it down:
1. The first term is:
  \e^{v_i}
2. The next term is another partial derivative:
  \pderiv{v_i}{\rho_i}
3. Then we have:
  (1-\e^{v_i})
4. Next we have to add on:
  +\e^{2v_i}
5. And finally we have:
  \pderiv{v_i}{\rho_i}
So the numerator is:
```
\e^{v_i}\pderiv{v_i}{\rho_i}(1-\e^{v_i})
  + \e^{2v_i}\pderiv{v_i}{\rho_i}
```
Inserting this into our code:

\[ \pderiv{^2\mathcal{L}}{{z_i^\rho}^2} = -\pderiv{\rho_i}{z_i^\rho} \left( \pderiv{v_i}{\rho_i} \frac{\e^{v_i}}{1-\e^{v_i}} + v_i \frac{\e^{v_i}\pderiv{v_i}{\rho_i}(1-\e^{v_i}) +\e^{2v_i}\pderiv{v_i}{\rho_i}}{(1-\e^{v_i})^2} \right) \]

⇦

⇧

⇨

This book is also available as A4 PDF or 12.8cm x 9.6cm PDF or paperback (ISBN 978-1-909440-00-5).